Tuttavia, per penetrare più a fondo la natura di questi fenomeni, è indispensabile combinare il metodo sperimentale con la teoria matematica"
(Carl Friedrich Gauss)
E' innegabile come SARS-CoV-2 sia il protagonista assoluto di questo periodo storico, che condiziona e condizionerà sicuramente anche in futuro le nostre vite.
Ma qui non vorrei parlare di lui e men che meno dei risvolti politici, psicologici, sociologici, economici e quant'altro che si porta dietro.
Non mi compete e non sono certo in grado di soffermarmi su queste complesse valutazioni che però sottendono comunque anche aspetti matematici, a volte correlati da modelli e dati statistici a volte legati a un immaginario collettivo.
La curva esponenziale del titolo ben si adatta ad esplicare questo legame con valutazioni di tipo statistico e di tipo potremmo dire "istintuale".
Si parla da tutte le parti, dai media, dagli esperti, dai ricercatori e così via di curve esponenziali senza spesso però valutarne il vero significato.
Incomincerei a descrivere quello che ho definito legame di tipo istintuale e che si riferisce alla cosiddetta infodemia.
Questo legame non è supportato da veri e attendibili dati ma identifica effettivamente una crescita di tipo esponenziale.
Per infodemia (dall'inglese infodemic, formata da information+epidemic) infatti si intende una straripante abbondanza di informazioni che rendono difficile comprendere la realtà dei fatti e che, come una metaforica epidemia di informazioni, soprattutto false o fuorvianti, si propagano, con il diffondersi su larga scala di una malattia infettiva, a ritmo esponenziale.
Quindi non si può definire una vera crescita esponenziale in senso matematico, ma se ne percepisce istintivamente una crescita esponenzialmente inarrestabile di ansia e panico, soprattutto grazie ai social, ai mezzi di comunicazione digitale, ove proliferano gli pseudoesperti, le voci infondate e la disinformazione.
Infodemic, parola d’autore, è stata infatti coniata da David J. Rothkopf e descrive, in un articolo del 2003 sul Washington Post, "When the Buzz Bites Back", lo sviluppo e gli effetti dell’epidemia di SARS, scoppiata in Cina nel novembre 2002, con conseguenze pesanti sull’economia, la politica e la sicurezza, non solo cinesi ma anche globali, del tutto sproporzionate rispetto agli effetti reali della malattia.
Sono passati 18 anni da quell'epidemia e stiamo assistendo ora a una vera pandemia.
Una valutazione sulla sua effettiva diffusione e pericolosità, mediata da un'infodemia proporzionata o sproporzionata, non è ovviamnete ancora possibile, ma si possono però, attraverso i dati raccolti via via, fare previsioni sul suo andamento?
E queste previsioni si possono basare su modelli e curve matematiche?
Costituisce un successo l'alleanza tra biologia e matematica, come sosteneva Gauss, il fatto che la modellizzazione matematica sia oggi alla base di decisioni di sanità pubblica riguardanti il controllo di malattie tradizionali ed endemiche, di infezioni emergenti e riemergenti così come è alla base della valutazione preventiva dell’impatto di malattie completamente nuove, appunto le cosiddette pandemie causate da un virus mutante, come può essere SARS-CoV-2.
Ovviamente una volta determinato il modello matematico che regola un fenomeno di natura biologica, è necessario attraverso una fase sperimentale e di recupero dei dati stabilire quanto il modello sia significativo.
Modelli e curve che a loro volta avrebbero bisogno, per una significativa e corretta previsione, di dati attendibili e, anche se quelli dell'ISS (le infografiche dell’Istituto Superiore di Sanità) hanno un buon margine di affidabilità, resta la mia riluttanza ad analizzare grafici o previsioni di "picco", basati su modelli matematici, che purtroppo non sono supportati da dati e rilevazioni davvero attendibili.
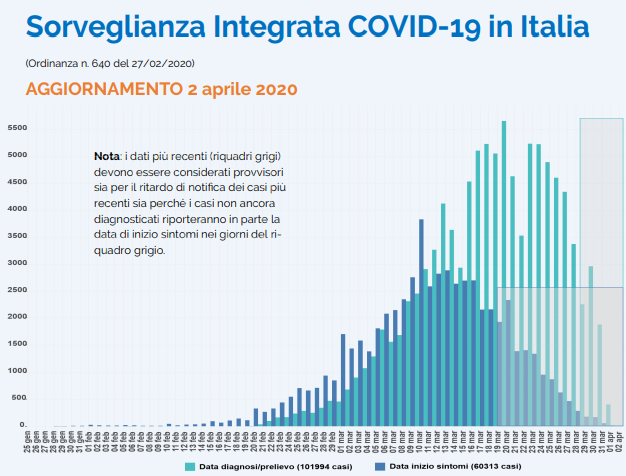
ISS - Andamento epidemico relativo al 2 aprile 2020
Qui vorrei invece fare un excursus storico/didattico sulla nascita e l'utilizzo di questi modelli matematici, di cui tra l'altro tutti ne parlano, senza magari sapere cosa effettivamente siano.
Un modello matematico nello studio di una epidemia serve principalmente a chiarificare le ipotesi, le variabili e i parametri che sono in gioco e per proporre di conseguenza parametri significativi per l’analisi e la classificazione delle epidemie stesse.
Utile se non determinante è la comprensione delle caratteristiche di trasmissione (Rzero, velocità di propagazione) della malattia infettiva per determinare le strategie migliori per ridurne la trasmissione, per prevederne il corso e paragonare l’efficacia di diverse misure di profilassi, quali quarantena, isolamento e trattamento.
In questo senso, i modelli matematici possono essere usati per pianificare, implementare e ottimizzare i programmi di individuazione, prevenzione, terapia e controllo dell'epidemia.
Daniel Bernulli (a sinistra) e Jean d’Alembert
Da buon illuminista, al celebre matematico parve che il modo migliore per dirimere la questione fosse quello di dimostrare in termini matematici esatti i vantaggi dell’inoculazione.
Bernoulli propose infatti un modello matematico fondato sulla crescita esponenziale del numero dei contagiati, dimostrando, sulla base di esso, che la vaccinazione sarebbe stata l'unica arma vantaggiosa per combattere la malattia.
Il lavoro di Bernoulli suscitò la discesa in campo di un altro celebre matematico, Jean d’Alembert, il quale, in una memoria pubblicata nello stesso anno (1760), pur condividendo, per ragioni ideologiche, l’opportunità dell’inoculazione, attaccò violentemente Bernoulli sul piano strettamente scientifico.¹
Egli non soltanto tentò di dimostrare l’inadeguatezza del calcolo delle probabilità nello studio di problemi come questo ma, in generale, manifestò il suo scetticismo per la matematizzazione, sottolineando però che le sue obbiezioni erano rivolte "soltanto ai Matematici che potrebbero affrettarsi troppo a ridurre questa materia in equazioni e in formule".
Comunque sia va dato merito al Bernulli di aver affrontato il problema epidemico quasi quarant'anni prima dell'introduzione del vaccino di Edward Jenner contro il vaiolo.
Gran parte però della teoria di base dell'epidemiologia matematica è stata sviluppata molto dopo tra il 1900 e il 1935 e da quel momento in poi c’è stato un graduale e costante progresso tanto nelle tecniche quanto nelle applicazioni.
Da allora si è diffuso l’uso di due modelli, deterministico e probabilistico, nell’analisi dello sviluppo di malattie infettive e si è grandemente sviluppato nel corso di tutto il ventesimo secolo fino ai giorni nostri.
Dopo i primi modelli a tempi discreti di Sir William Heaton Hamer (1906) e di Ronald Ross (premio Nobel per la Medicina 1902, lavori sulla prevenzione della malaria del 1911), negli anni venti, William Ogilvy Kermack e Anderson Gray McKendrick proposero un modello di tipo differenziale (il cosiddetto SIR) per spiegare la rapida crescita e successiva decrescita del numero di persone infette osservate in alcune epidemie, come la peste (Londra 1665-1666, Bombay 1906) e il colera (Londra 1865).
Questo modello matematico sviluppato nel 1927 dagli scienziati William Ogilvy Kermack e Anderson Gray McKendrick, sarà destinato a diventare uno dei principali punti di riferimento per lo studio e l'elaborazione dei modelli di diffusione epidemica.
Tipico andamento di una epidemia secondo lo schema SIR - foto dall'articolo di
Paolo Alessandrini "La matematica delle epidemie"
Dove i suscettibili sono gli individui sani ma soggetti a pericolo di contagio, gli infetti sono gli ammalati, e i rimossi sono gli individui non più infetti, e dunque immuni, o perché guariti o perché morti.
Dalla seconda metà del ventesimo secolo, il numero di modelli e di studi matematici in quest’ambito è aumentato a dismisura e, in epoche più recenti, sono stati utilizzati modelli per valutare l’effetto di strategie di controllo delle epidemie di afta epizootica in Gran Bretagna nel 2001 o l’epidemia di SARS (Severe Acute Respiratory Syndrome) del 2002-2003 o quelle di febbre emorragica da Ebola che nel 2014 hanno interessato Liberia, Guinea e Sierra Leone.
L’epidemiologia matematica differisce da buona parte della matematica applicata poiché non si presta a validazioni sperimentali dei modelli proposti, in quanto gli esperimenti sono generalmente impossibili (ed ovviamente non etici), e quindi tali modelli vengono testati su episodi passati.
Questo dà molta importanza alla modellizzazione matematica come un possibile strumento predittivo per fronteggiare in tempo reale lo scoppio di un’infezione, che può essere epidemica o addirittura pandemica.Come detto, esistono due approcci per la formulazione di modelli matematici in questo ambito, uno probabilistico e l’altro deterministico.
Il primo modello risulta sicuramente più ricco di informazioni e più corretto da un punto di vista metodologico, ma proprio per questo più difficile da studiare matematicamente. Il secondo che si basa su equazioni differenziali, richiede meno dati e si sviluppa seguendo l'asserto che il processo epidemico sia con buona approssimazione deterministico.
Tornando al modello di Kermack e McKendrick, troviamo una prima versione del Teorema della Soglia Critica, di quello che svilupperà in seguito lo statistico inglese Maurice Kendall (1956 approccio di Kendall all'epidemia "generale") che permette di individuare un parametro critico σ (o Rzero), che dipende dalle costanti caratteristiche del modello e, in linea di principio, determinabile statisticamente.
Se σ ≤ 1 (con σ si identifica Rzero, velocità di propagazione), la malattia non supera il numero di infetti dell’istante iniziale e quindi decade a zero senza diffondersi in maniera drammatica attraverso la popolazione, se σ > 1, la malattia è sufficientemente forte da riuscire a diffondersi attraverso la popolazione. Più è grande il valore di σ e più la malattia sarà da considerarsi virulenta.
Anderson Gray McKendrick (a sinistra) e William Ogilvy Kermack
E' interessante storicamente porre l'attenzione sul contributo alla diffusione di modelli biologici di tipo differenziale che si deve appunto a William Ogilvy Kermack e Anderson Gray McKendrick, che tra il 1927 e il 1933 pubblicarono uno studio matematico in tre parti, intitolato "A contribution to the mathematical theory of epidemics"
Anche se il modello contiene ipotesi irrealistiche, i concetti introdotti risultarono essenziali per fornire una prima valutazione intuitiva sulla dinamica delle epidemie, intuizione che comunque rimane confermata in modelli attuali anche se modificati e più complessi.
Essi si proponevano di indagare sulle dinamiche di diffusione di alcuni tipi di malattie infettive fra la popolazione e miravano a spiegare l’andamento apparentemente anomalo di epidemie, come quella di peste nell’isola di Bombay (1905-1906), in cui si era osservato che il numero di persone infette subiva una rapida crescita seguita da una decrescita inaspettata.
Una delle domande alla quale cercarono di dare una risposta era:
"Nel caso in cui un’epidemia si estingua, l’estinzione stessa è da imputarsi necessariamente all’esaurimento degli ospiti infettabili oppure è possibile che una pandemia termini lasciando salvo un gruppo consistente di individui non immuni e mai contagiati?"
A tale scopo nella prima parte del loro studio Kermack e McKendrick proposero un sistema differenziale non lineare del prim’ordine, che è divenuto appunto noto come modello epidemico di tipo SIR e che si applica allo studio di malattie infettive che, nel caso in cui il malato riesca a sopravvivere e guarire, conferiscono all’ospite l’immunità da un nuovo contagio, come succede per esempio con la febbre emorragica da Ebola, quella che si potrebbe definire "immunità di gregge", immunità divenuta drammaticamente popolare per le parole del Primo Ministro del Regno Unito Boris Johnson.²
Il vero problema iniziale consiste nel riuscire a valutare correttamente la velocità di propagazione che, dipendendo da dati statistici rilevati, non è facilmente determinabile ad epidemia in corso e qualsiasi modello non è in grado di cogliere quando cambi la curva dei contagi per una epidemia nuova ed è fondamentale capire su cosa si basino i modelli predittivi che vengono suggeriti e basati su equazioni statistiche.
Essendo nell’universo della probabilità e non della certezza, servirebbero quindi molte più informazioni di quelle che si hanno, per esempio oggi sul Covid-19, per farne previsioni davvero attendibili.
Per modellare correttamente questa epidemia si dovrebbe tener conto oltre che del σ (o Rzero), di altri parametri quali: il tempo di incubazione, il tempo in cui il soggetto è asintomatico, la durata della patologia, le modalità di trasmissione...
Tutte variabili difficilmente valutabili essendo in presenza di un virus di cui si conosce davvero troppo poco.
Secondo le stime attuali, ciascun contagiato può infettare almeno due persone, che a loro volta infettano altrettante persone, in pratica uno scenario che potrebbe rivelarsi valido per l’Italia con un σ=2,6 (in base a uno studio dell’ospedale Sacco di Milano), o σ=2,2 (in base ad altri studi).
Senza contare anche il fatto che non sappiamo quanti sono gli asintomatici, gli infetti con sintomi lievi, gli immuni o il numero effettivo di decessi e quindi qualunque modello matematico di tipo SIR non può dare previsioni attendibili.
Immagine dall'articolo "La matematica delle epidemie: istruzioni per l’uso",
di Andrea Pugliese
Per conoscere in dettaglio le procedure matematiche per ottenere questi modelli o la determinazione del valore Rzero, che può essere più o meno complessa, lascio qui il link a un interessante approfondimento tematico, proprio in riferimento alla situazione attuale dell'epidemia di Covid-19, "La matematica delle epidemie: istruzioni per l’uso", di Andrea Pugliese, professore di analisi matematica presso l’Università di Trento, che è il maggior studioso italiano di modelli matematici per le epidemie.
Note
¹ Da un'interessante articolo del grande Giorgio Israel, storico della scienza, matematico ed epistemologo italiano dal titolo "Oltre il mondo inanimato: la storia travagliata della matematizzazione dei fenomeni biologici e sociali"
² "Il 60% dei britannici dovrà contrarre il Coronavirus per sviluppare l'immunità di gregge" queste le parole shock pronunciate inizialmente dal Premier Boris Johnson, poi ritrattate. Articolo di La Repubblica







Nessun commento:
Posta un commento