"Nella relatività generale la materia è un buco in un pieno: più precisamente, una discontinuità del campo gravitazionale. Nei luoghi in cui si trova la materia il campo diventa infatti infinito, e cessa dunque di esistere."
Immagine dalla copertina del libro "Il Vangelo secondo la Scienza" dove
Piergiorgio Odifreddi scrive questa frase per descrivere la materia
come una discontinuità del campo gravitazionale (pag 64).
"Più che di macchie si dovrebbe parlare d'un manto nero la cui uniformità è spezzata da nervature chiare che s'aprono seguendo un disegno a losanghe: una discontinuità di pigmentazione che già annuncia la discontinuità dei movimenti. A questa punto la bambina del signor Palomar, che si è stancata da un pezzo di guardare le giraffe, lo trascina verso la grotta dei pinguini. Il signor Palomar, cui i pinguini dànno angoscia, la segue a malincuore…"
Immagine relativa alla frase scritta da Italo Calvino nel suo Palomar,
un romanzo pubblicato per la prima volta nel 1983,
Frase in cui descrive la discontinuità del manto di una giraffa
L’"Indennità di discontinuità", destinata a musicisti, attori, autori e tecnici del settore, è un disegno di legge approvato il 18 maggio scorso dal Senato della Repubblica Italiana avente ad oggetto l’indennità di discontinuità per i lavoratori dello spettacolo che rappresenta una sorta di reddito che copre tutti i lavoratori dello spettacolo nei momenti di inattività oppure durante il periodo di studio e di formazione.
Immagine relativa al disegno di legge
"Vedere il mondo come fondamentalmente continuo contrasta nettamente con il vederlo come fondamentalmente discontinuo. Un mondo continuo rappresenta il sogno newtoniano-laplaciano di un graduale e costante movimento verso l'alto della realtà attraverso un dolce processo evolutivo darwiniano.
In economia questo punto di vista è stato incarnato da Alfred Marshall.
Un mondo discontinuo si caratterizza in netti contrasti e improvvisi cambiamenti come nella moderna, teoria evolutiva di Niles Eldredge e Steven Jay Gould (1972).
In economia questo punto di vista è stato affermato in modo più eloquente da Karl Marx e Joseph Schumpeter."
Immagine, relativa alla discontinuità in economia, della copertina del libro
"Nella storia di una democrazia la discontinuità è un elemento fecondo e non un baratro di cui aver paura"
Questa frase, attribuita al giornalista Paolo Mieli, sintetizza la discontinuità in democrazia.
Cinque esempi di discontinuità, per introdurre il tema, appunto "discontinuità" del Carnevale della Matematica n°165, di gennaio 2023.
Ma il termine "discontinuità" ha moltissimi altri usi e significati che anche la stessa definizione dell'enciclopedia Treccani non può ricoprire:
"Mancanza di continuità, interruzione nel tempo o nello spazio: d. di movimento; d. della tradizione; d. di una superficie, ecc.; anche in senso fig., di cosa che non sia continua, coerente, unitaria nelle sue manifestazioni o qualità: d. di metodo; d. di tono, di stile; d. di un racconto, di un discorso, ecc. In fisica, variazione brusca, nello spazio o nel tempo, di una grandezza fisica; punto di d., ogni punto dello spazio in cui si verifichi una discontinuità di una determinata grandezza (per estens., anche riferito al diagramma della grandezza); superficie di d. e linea di d., superficie e linea, rispettivamente, luogo di punti di discontinuità. In meteorologia, presenza di due masse contigue di aria a caratteri differenti, affiancate o sovrapposte, separate da una superficie detta appunto superficie di discontinuità. In geofisica, superfici di d. sismica, quelle che separano gli involucri concentrici, di diversa composizione chimico-mineralogica e di diverso stato fisico, che costituiscono il globo terrestre; si dicono di primo o di secondo ordine, a seconda che ad esse corrisponda un cambiamento repentino o graduale di velocità delle onde sismiche. In matematica, punto di d. di una funzione, punto in cui la funzione non è continua".
Di interesse scientifico, in statistica, biostatistica, econometria, scienze politiche, epidemiologia, psicologia, pedagogia e discipline correlate, troviamo il "Disegno di Discontinuità di Regressione" (RDD - Regression Discontinuity Design) o Progettazione della Discontinuità di Regressione, che è un metodo di inferenza causale, visto come un metodo utile per determinare se un programma o un trattamento è efficace.
Questo metodo si concentra sulle caratteristiche delle osservazioni su entrambi i lati di una soglia definita dal ricercatore.
E' un disegno considerato quasi-sperimentale, che mira a determinare l'efficacia di un trattamento confrontando tra fase pre-test e post-test che isola gli effetti causali di intervento assegnando un valore di soglia al di sopra o al di sotto il momento di somministrazione dell'intervento.
Applicato per la prima volta da Donald Thistlethwaite e Donald Campbell per valutare l'effetto delle borse di studio, il suo utilizzo è aumentato di recente.
La sua rilevanza è stata confermata confrontando i risultati ottenuti con questa tecnica con quelli ottenuti tramite studi randomizzati controllati e l'RDD è diventato, negli ultimi anni, sempre più popolare come metodo nella valutazione delle politiche pubbliche.
Altre discontinuità interessanti sono, in geologia, quelle di Mohorovičić, di Gutenberg o di Lehmann
La "Discontinuità di Mohorovicic", o "Moho", rappresenta il confine tra la crosta e il mantello terrestre.
In geologia la parola "discontinuità" è usata per una superficie nella quale le onde sismiche cambiano velocità. Una di queste superfici esiste a una profondità media di 8 chilometri sotto il bacino oceanico e a una profondità media di circa 32 chilometri sotto i continenti, e a questa discontinuità, le onde sismiche accelerano.
Questa discontinuità detta di Mohorovicic è stata scoperta nel 1909 da Andrija Mohorovicic (Volosca, 23 gennaio 1857 – Zagabria, 18 dicembre 1936), un sismologo croato che si rese conto che la velocità di un'onda sismica è correlata alla densità del materiale attraverso il quale si muove.
Interpretando l'accelerazione delle onde sismiche osservate all'interno del guscio esterno della Terra come un cambiamento compositivo all'interno della Terra, comprese che l'accelerazione deve essere causata da un materiale di maggiore densità presente in profondità.
Il materiale di densità inferiore immediatamente sotto la superficie è ora comunemente indicato come "crosta terrestre" e il materiale ad alta densità sotto la crosta come "mantello terrestre".
La "Discontinuità di Mohorovicic" segna quindi il limite inferiore della crosta terrestre.
Mohorovicic ha potuto utilizzare la sua scoperta per studiare le variazioni di spessore della crosta, scoprendo che la crosta oceanica ha uno spessore relativamente uniforme, mentre la crosta continentale è più spessa sotto le catene montuose e più sottile sotto le pianure.
C) Discontinuità di Lehmann
1) Crosta continentale 2) Crosta oceanica 3) Mantello superiore
4) Mantello inferiore 5) Nucleo esterno 6) Nucleo interno
La "Discontinuità di Gutenberg" è la superficie che separa il nucleo dal mantello all'interno della Terra, individuata e scientificamente determinata per la prima volta nel 1914 dal geofisico tedesco Beno Gutenberg (Darmstadt, 4 giugno 1889 – Pasadena, 25 gennaio 1960).
Col nome "Discontinuità di Lehmann" si indicano due differenti discontinuità nella struttura interna della Terra, entrambe scoperte dalla sismologa danese Inge Lehmann (Copenaghen, 13 maggio 1888 – Copenaghen, 21 febbraio 1993).
Le caratteristiche dettagliate del mantello superiore terrestre tra Moho e la zona di transizione sono ancora poco conosciute. Una questione importante è l'esistenza e la natura della discontinuità di Lehmann a 220 km di profondità, che è stata scoperta all'inizio degli anni '60 e di cui è stata recentemente confermata l'esistenza sia nelle regioni continentali che oceaniche.
Lascio al lettore (ai link evidenziati) altre curiosità sulle discontinuità geologiche qui, ovviamente per il Carnevale della Matematica, mi soffermerò a illustrare una discontinuità matematica.
In matematica esistono molteplici branche che analizzano i fenomeni discontinui e i diversi metodi includono la teoria delle catastrofi, la teoria del caos, la geometria frattale, la teoria della sinergia, la criticità auto-organizzante...e tutti, in un modo o nell'altro, sono stati applicati in molteplici campi.
Non voglio certo, in questa sede, affrontare tematiche così complesse ma più semplicemente solo soffermarmi sulla discontinuità delle funzioni, facendo un breve accenno storico legato alla nascita del concetto di limite.
Ritratto di Gottfried Wilhelm von Leibniz conservato
presso la Biblioteca regionale di Hannover
Prima di addentrarmi nel secolo, l'ottocento, che ci porterà ad avere in mano la quasi definitiva definizione di limite (e quindi di concetto di continuità e discontinuità di una funzione) mi soffermerei un momento sul secolo dei "lumi", che ha portato all'evoluzione del fondamentale concetto per lo sviluppo dell'analisi infinitesimale, il concetto appunto di funzione.
Il primo a introdurre il termine "funzione" relativamente all'applicazione del calcolo alle curve, fu, tanto
per cambiare, Leibniz, in un manoscritto del 1673 che riportava tale termine direttamente nel titolo, "Methodus tangentium inversa seude functionibus".
Questo concetto ritorna ancora ripetutamente nella corrispondenza che Leibniz tenne con i Bernoulli fra il 1692 e il 1694.
Ma fu "Introductio Analysin In
nitorum", del 1748 di Eulero, la prima opera in cui il concetto di funzione ebbe un ruolo esplicito e centrale. Nella prefazione, Eulero afferma che l'analisi matematica è la scienza generale delle variabili e delle loro funzioni.
Inizia definendo una funzione come "espressione analitica" (cioè una "formula"):
"Una funzione di una quantità variabile è un'espressione analitica composta in qualsiasi modo da quella quantità variabile e numeri o quantità costanti"
Sebbene la nozione di funzione non sia originata da Eulero, fu lui a darle il primo risalto trattandone il calcolo come una teoria formale delle funzioni.
Nel secondo volume dell' "Introductio" Eulero da un'ulteriore distinzione tra funzioni dando la seguente definizione di funzione continua e discontinua:
"La linea curva continua è quella la cui natura è espressa da una sola funzione determinata di x. Se però la linea curva è composta da differenti parti determinate da più funzioni di x, di modo che una parte sia il risultato di una funzione e un'altra sia il risultato di una seconda funzione, noi chiamiamo queste specie di linee curve discontinue, o miste e irregolari, giacché esse non sono formate secondo una legge costante e sono composte di porzioni di differenti curve continue".
Vibrazione corda nel piano
Il concetto di funzione diventa centrale quindi verso la metà del Settecento grazie ad una questione di carattere fisico-matematico: studiare le vibrazioni di una corda in un piano.
Ed è proprio da questi studi fatti da vari matematici, tra cui Jean-Baptiste D'Alembert, Joseph-Louis Lagrange e Joseph Fourier, che la discussione si andrà ad incentrare sulla questione strettamente matematica del concetto di funzione, che si intendeva allora nella definizione "standard" data da Euler, ed in particolare sulla continuità o discontinuità di queste funzioni.
Fu addirittura indetto un concorso dall'Accademia di Pietroburgo, nel 1787, per determinare la natura di queste funzioni, che fu vinto nel 1791 da Louis François Arbogast, che diede una prima definizione di funzione continua, distinguendo due casi in cui le funzioni non rispettavano questa continuità: in un primo caso può "cambiare del tutto" la "legge secondo cui la funzione dipende dalla variabile”, e avremo una funzione che egli chiama discontinua, oppure si può avere il caso che "differenti parti di una curva non si congiungono fra loro", ed in questo caso avrò una funzione
discontigua.
Si può notare come si stessero già insinuando, all'interno del calcolo infinitesimale, quei concetti che, pur essendo ancora ben lontani dal rigore con cui li utilizziamo oggi, risultano necessari per la formalizzazione rigorosa di quel "calcolo sublime" che ha ideato Leibniz, ed in particolare per il concetto di limite su cui esso fonda le sue basi.
Sarà l'opera di Lagrange, "Théorie des fonctions analytiques" datata 1797, ad aprire le porte al nuovo secolo e alla sua grande ricerca in termini di analisi infinitesimale, dando un fondamento rigoroso al calcolo, allontanandolo il più possibile dalle evidenze di tipo geometrico.
Come preannunciato da Lagrange, la riorganizzazione delle teorie matematiche in funzione della didattica fu la grande spinta che porterà i matematici a ricercare, e conferire infine, quel rigore e quella struttura che da tempo si cercava.
A partire dunque da Luis Cauchy e Niels Abel, e prima di lui già con Bernard Bolzano, si assiste così all'inizio del processo che porterà ad affermare l'analisi come branca della matematica autonoma e poggiata su principi rigorosi e profondi.
Proprio la ricerca in questa direzione porterà al più grande e profondo sviluppo che la matematica in generale abbia mai avuto, e con essa le grandi applicazioni in campo fisico e tecnologico alle quali ha condotto.
Questo il motivo per cui l' Ottocento verrà designato come il secolo dell' "età dell'oro della matematica", basti anche pensare ai nomi dei grandi matematici che vi hanno contribuito: Carl Friedrich Gauss (1777 – 1855), Augustine-Luis Cauchy (1789 – 1857), Peter Gustav Dirichelet (1805-1859), Évariste Galois (1811 – 1832), Carl Weirstrass (1815 – 1897), Bernhard Riemann (1826 – 1866), Richard Dedekind ( 1831 – 1916), Georg Cantor (1845 – 1918), Henri Poincaré (1854 – 1912)...
Il "Cours d'analyse" di Luis Cauchy tratta per lunghe pagine lo studio dei "valori singolari delle funzioni in alcuni casi particolari", ovvero dopo aver definito i punti in cui la funzione è continua, va a studiare i principali casi di discontinuità, che lo stesso Cauchy definisce "una delle questioni più importanti e delicate dell'analisi".
Avendo ricondotto tutto al concetto di limite, ovviamente per studiare le singolarità occorrerà andarne a studiare i limiti.
Passando per Dedekind e Cantor, alla fine dell'Ottocento, il formalismo e la ricerca del rigore iniziato alla fine del Settecento trovano finalmente il loro coronamento.
Il concetto di limite si fonde con quello di continuità e all'inizio del Novecento ritroviamo, grazie alla sempre più netta distinzione fra scuole di pensiero formaliste o meno, la definizione di limite come oggi cerchiamo di farla imparare ai nostri studenti, cioè formalizzata al massimo con la notazione ε-δ che già era stata introdotta da Carl Weirstrass ed Eduard Heine, e che troverà la sua attuale e definitiva definizione in un articolo apparso nel 1922 sul American Journal of Mathematics intitolato appunto "A General Theory of Limits", scritto da E.H.Moore e H.L .Smith.
Libro Analisi 1 (seconda parte) di Giovanni Ricci a pag 178
Aprendo il volume di Analisi 1 (seconda parte) del mio mitico Professore Giovanni Ricci a pag 178 si trovano le definizioni di discontinuità legate strettamente al concetto di limite.
Va comunque tenuto presente che non c'è uniformità nella letteratura scientifica sulla definizione di punto di
discontinuità.
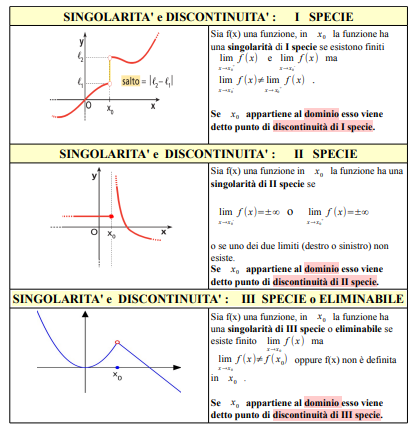
Molti definiscono il concetto di discontinuità come sinonimo di punto singolare, mentre secondo le definizioni dell'immagine l'appellativo di punto di discontinuità è riservato ai punti singolari appartenenti al dominio della funzione.
Classificazione delle discontinuità delle funzioni
Concludo qui, con queste note matematiche le mie osservazioni su un tema, quello della "discontinuità", che certamente abbraccia tutto un mondo di sfaccettature e di concetti, impossibili da sviscerare in un breve articolo.