Se uniamo anche il fatto che lo stesso Flavio Ubaldini ricordava che questo Carnevale avrebbe avuto anche una sua melodia, sibillinamente commentando "sarà razionale o sarà irrazionale?"
Beh non avrebbe potuto che essere uno dei numeri irrazionali più affascinante, il "Φ".
L'irrazionalità e la melodia non potrebbero meglio compenetrarsi se non in questo "numero d'oro", in questo "numero magico", in questo "golden ratio" che è veramente unico nelle sue proprietà matematiche e che pervade soprattutto l'arte, l'architettura e il design, la musica, la finanza........tutta la natura stessa.
Ciò che rende Φ molto più di un interessante numero irrazionale è che appare davvero in tutta la natura.
Si trova nelle proporzioni del viso e del corpo umano e di quello di molti altri animali , nella struttura delle piante, nel sistema solare.....nei rapporti musicali e nelle dimensioni degli strumenti, nei rapporti architettonici e pittorici......fino ad arrivare anche alle variazioni di prezzo e tempi dei mercati azionari o persino alla fede e ai luoghi sacri.
Il suo interesse non riguarda solo quindi i matematici, ma spazia dai naturalisti, ai medici, agli astronomi, ai pittori, agli architetti, ai musicisti.......fino agli investitori e ai mistici.
Cosa ci dice la Storia?
Cerchiamo di scoprire, prima delle sue proprietà matematiche, la sua origine e la sua storia iniziata 5000 anni fa.
Le prime applicazioni del rapporto aureo, risalgono agli antichi Egizi, anche se non ne è stata ritrovata una precisa definizione.
Nella stele del re Get, proveniente da Abido (antica capitale dell’ Egitto nel periodo predinastico) conservata oggi al Louvre, si osserva al centro un rettangolo aureo, nella cui parte bassa il quadrato costruito sul lato più corto, sezione aurea di quello più lungo, contiene la città mentre nella parte rimanente, che è ancora un rettangolo aureo, è riportato il serpente simbolo del re.
Il reperto risalirebbe alla prima dinastia, quindi a quasi 5000 anni fa. Altri studi dimostrano che la sezione aurea fu anche applicata nella costruzione delle piramidi.
Il concetto di "proporzione" nacque infatti nel contesto della dottrina pitagorica, introdotta in Grecia appunto da Pitagora di Samo, agli albori della filosofia occidentale, quando la visione mitologica si andava trasformando attraverso l’interpretazione razionale nella ricerca del principio unico e universale, l'origine del tutto.
Soprattutto dallo studio delle leggi numeriche che regolavano l’armonia musicale la scuola pitagorica scoprì alcuni principi morfologici di carattere generale, che divennero presto i principi compositivi di ogni tipo di arte, soprattutto quella che si occupava della costruzione degli edifici sacri.
Gli antichi architetti dovevano infatti realizzare, il cosiddetto “accordo delle misure”, vale a dire la ricerca di simmetrie mediante il ripetersi di certi rapporti proporzionali privilegiati e l’"Eurytmia", cioè l'armonia tra le lunghezze, le superfici e i volumi dell’edificio, sia nel complesso che nelle sue singole parti. Mediante quindi una tecnica compositiva di tracciati regolatori e di raffinate costruzioni geometriche e partendo dalla forma iniziale, un quadrato, erano così in grado di individuare, con semplici proiezioni e ribaltamenti, tutte le linee principali dell’edificio.
Il Partenone fu costruito tra il 447 e il 438 a.C. su progetto di Ictinio e Callicrate ed adornato dalle sculture di Fidia. Proprio dalla lettera iniziale del grande scultore, nel XX secolo, il matematico americano Mark Barr ha introdotto, Φ (phi) per indicare il rapporto aureo.
Fra Luca Pacioli e Piero della Francesca
Tra questi artisti e matematici spiccano:
- Leon Battista Alberti (1404-1472)
- Piero della Francesca (1416-1492)
- Luca Pacioli (1445-1517)
- Leonardo da Vinci (1452-1519)
Anche se indagini effettuate con diagrammi e rigorose riproduzioni hanno messo in evidenza che questa "Divina Proporzione" sia stata la regola che dominava la connessione di tutte le parti di molte sue costruzioni, Leon Battista Alberti non parlò mai, nei suoi trattati, del tipo di proporzionamento utilizzato.
Il Tempio Malatestiano a Rimini è comunque un significativo esempio del "metodo segreto" con cui l'Alberti riusciva ad ottenere quell’armonioso equilibrio.
Per tutto il Rinascimento quindi il Φ rappresentò un canone di bellezza a cui ispirasi per ogni composizione artistica, dall’architettura, alla scultura, alla pittura di cui ne sono un esempio i dipinti di Piero della Francesca o di Leonardo da Vinci.
La Flagellazione di Piero della Francesca
L'ultima cena di Leonardo da Vinci
Leonardo da Vinci ne fece il pilastro della sua imponente produzione e collaborò, con perfette tavole e bellissimi disegni, alla stesura dell'opera di Luca Pacioli di cui era amico dai tempi della loro collaborazione milanese al servizio di Ludovico Sforza.
Da una parte l’ interesse prevalente di Leonardo era l’ estetica e la sezione aurea soddisfaceva entrambi i punti di vista, matematico ed artistico, dall'altra nessun altro matematico ha più potuto vantare una collaborazione più eccellente.
Fu quindi proprio l’opera di Luca Pacioli, “La Divina Proportione”, stampata e diffusa in tutta Europa, a diffondere questa concezione incentrata proprio sulla proporzione come chiave universale per penetrare i segreti della bellezza ma anche della natura.
Nel trattato si trova un pò di tutto. Nel Rinascimento infatti non vigeva ancora la specializzazione moderna del sapere e un uomo colto trattava indifferentemente astronomia, filosofia, prospettiva, pittura, musica, architettura e matematica, anche se poi inevitabilmente finiva con l’ eccellere solo in alcune.
L’ opera di Pacioli, “Divina Proportione”, fu pubblicata a Venezia nel 1509 in tre volumi e, con la precedente “Summa de arithmetica, geometria, proportioni et propotionalità”, un sommario della matematica di quel tempo, insieme ad una traduzione in latino degli Elementi di Euclide, contribuì alla rinascita della Scienza in Europa attraverso la riscoperta di Euclide ed Archimede con i loro metodi logico-deduttivi.
L’ ammirazione che il Pacioli aveva per questa costruzione era tale da indurlo a metterla in relazione con la Divinità, come la quale è una e trina: "Tra tutte le possibili proporzioni, quella aurea sembra essere la vera ispiratrice della bellezza, quindi del creato, quindi del Suo creatore, quindi Divina"
Fra Luca Pacioli consegna il manoscritto "Divina Proportione" a Ludovico Sforza
.
Nel Rinascimento riemerge la convinzione che l’architetto non sia in nessun modo libero di applicare all’edificio uno schema casuale di rapporti, ma che tali rapporti debbano invece conciliarsi con un sistema di ordine superiore, in cui le proporzioni riescano ad esprimere l’ordine cosmico.
Altre applicazioni del Golden Ratio in architettura possono essere viste in Notre Dame a Parigi, nel Duomo di Milano, nell' edificio sede delle Nazioni Unite a New York o nella CN Tower di Toronto e nel Modulor di Le Corbusier.
"Le Modulor" è un sistema, basato sulle misure umane, la doppia unità, la sequenza di Fibonacci e la sezione aurea, e fu introdotto da Le Corbusier ("Le Modulor" nel 1948, seguito da "Le Modulor 2" nel 1955) che lo usò nella progettazione di molti edifici per migliorare sia l'estetica che la funzionalità dell'architettura.
La "Divina Proporzione" è comunemente usata nella progettazione di prodotti e loghi di molte grandi aziende o nel design di alta moda, come nella "Phi Collection" prodotta dal 2004 da Vogue, Elle e Vanity Fair.
Cosa ci dice la natura?
Ci sono molte altre affascinanti relazioni matematiche e stranezze sia di Φ che della serie di Fibonacci che andrebbero esplorate in modo più approfondito, ma per ora diamo una breve occhiata avventurandoci nella natura, dove appunto sia Φ che la serie di Fibonacci si manifestano pervasivamente.
I numeri di Fibonacci appaiono spesso nel numero dei petali in un fiore, nelle posizioni e nelle proporzioni delle dimensioni chiave di molti, se non la maggior parte, degli animali. Alcuni esempi sono le sezioni del corpo di formiche e altri insetti, le spirali di conchiglie di mare e la posizione delle pinne dorsali delle focene. Persino le spirali del DNA umano incarnano proporzioni Φ.
Più interessante ancora è l'ampio aspetto di Φ in tutta la forma umana, il viso, il corpo, le dita, i denti...... e l'impatto che questo ha sulla nostra percezione di umana bellezza. Alcuni potrebbero sostenere che la bellezza è negli occhi di chi guarda, ma si potrebbe anche dimostrare che ciò che percepiamo come bellezza delle donne e degli uomini si basi su un rapporto di proporzioni tra viso e corpo strettamente legato a Φ. Sembra infatti che Φ sia l'hard-wired nella nostra coscienza come guida alla bellezza.
Per questo motivo, Φ viene applicato sia in chirurgia plastica facciale sia in odontoiatria estetica come guida per ottenere i risultati più naturali e armoniosi delle caratteristiche facciali e corporee.
Se moltiplichiamo per Φ (1,618.....) la distanza che, in una persona adulta, va dai piedi all'ombelico, otteniamo la sua statura. Così la distanza dal gomito alla mano (con le dita tese) moltiplicata per Φ, da la lunghezza totale del braccio o come la distanza che va dal ginocchio all'anca, moltiplicata per Φ, dà la lunghezza della gamba, dall'anca al malleolo. Anche nella mano i rapporti tra le falangi delle dita medio e anulare sono aurei, così come il volto umano è tutto scomponibile in una griglia i cui rettangoli hanno i lati in rapporto aureo.
Sono stati condotti diversi studi per dimostrare se un rettangolo aureo sia il rettangolo più piacevole per l'occhio umano e i risultati degli studi generalmente indicano che le forme più vicine al rettangolo aureo siano effettivamente le più gradevoli.
Già nel 1875 lo psicologo tedesco Fechner sottopose a più persone un insieme di rettangoli, chiedendo poi di indicare quale rettangolo avesse destato in loro una maggiore sensazione di armonia.
Grafico della distribuzione percentuale delle preferenze registrate
da Fechner.
L’esperienza di Fechner sanzionava quindi un’opinione largamente diffusa tra pittori, architetti e matematici secondo cui dall’osservazione del rettangolo aureo si trae un senso di equilibrata armonia.
Senza dimenticare l'armonia nella musica. La stessa musica ha fatto spesso uso della sequenza di Fibonacci, come nelle fughe di Bach, nelle sonate di Mozart, o nelle “33 variazioni sopra un valzer di Dabelli”, in cui Beethoven suddivise la sua composizione in parti corrispondenti ai numeri di Fibonacci.
Insomma, il rapporto Φ (1.618...) o il suo inverso (0.618...) sono simbolo dell’armonia delle costruzioni dell’uomo e la sequenza da cui deriva può regalare assonanze e melodie sublimi.
Il primo incontro con la "Divina Proportione" in genere avviene in Geometria.
Trattasi infatti della proposizione 11 del libro II degli Elementi di Euclide che recita così: "Come dividere un segmento in modo che il rettangolo che ha per lati l’ intero segmento e la parte minore sia equivalente al quadrato che ha per lato la parte maggiore”, ovvero come trovare la Sezione Aurea di un segmento, cioè la parte media proporzionale tra l’ intero segmento e la parte rimanente.
Queste le due classiche dimostrazioni:
AD : AB = AB : AE
(AD-AB) : AB = (AB – AE) : AE
AS : AB = SB : AS
AB : AS = AS : SB
AS : DB = CA : BS
AS : AB = AB : (AS – AB)
Ma tante altre sono le caratteristiche della Sezione Aurea , sempre geometriche, e una delle più importanti è la seguente: “Se in un triangolo isoscele la base è la sezione aurea del lato allora l’ angolo al vertice è un quinto dell’ angolo piatto, ovvero la base è il lato del decagono regolare inscritto nel cerchio che ha per raggio il lato”
Il valore algebrico (ovvero soluzione di un'equazione polinomiale a coefficienti interi) che esprime la "sezione aurea" (0,618034) o il "numero aureo" (1,618034), è un numero irrazionale (cioè non rappresentabile come frazione di numeri interi).
In un diagramma cartesiano una retta rappresenta una crescita lineare, cioè una crescita nella quale l’ incremento si ottiene “sommando” a quanto raggiunto sempre la stessa quantità.
Una crescita invece in cui l’ incremento si ottiene moltiplicando quanto raggiunto per una
quantità a questo proporzionale si dice quadratica ed è rappresentato da una parabola
I due diagrammi si incontrano in un punto che determina con gli assi cartesiani un rettangolo aureo, quasi a significare l’ equilibri tra una crescita lineare ed una crescita quadratica.
Ma Φ può essere approssimato, con crescente precisione, anche dai rapporti fra due termini successivi della successione di Fibonacci, a cui è strettamente collegato.
Nel "Liber Abaci" ("Il Libro dell’Abaco") Fibonacci espone i fondamenti di algebra e matematica usati nei paesi arabi.
La risoluzione di un problema gli fornì l’occasione per l’introduzione della successione (di Fibonacci) che ha uno strettissimo legame appunto con il Numero Aureo.
E' una successione di numeri interi positivi, definita per ricorrenza, in cui ciascun numero è la somma dei due precedenti e i primi due termini della successione sono per definizione F1=1 e F2=1. Tale successione ha quindi una definizione ricorsiva secondo la seguente regola:
F1=1
F2=1
Fn=F{n-1}+F{n-2}
Foglio del manoscritto su pergamena del Liber abbaci conservato nella Biblioteca Nazionale Centrale di Firenze contenente nel riquadro a destra le prime tredici cifre, in numeri arabi, della cosiddetta "successione di Fibonacci"
Analizziamone alcune proprietà¹:
Il rapporto 
, per 
tendente all'infinito, tende al numero algebrico irrazionale 
chiamato sezione aurea o numero di Fidia.
, per tendente all'infinito, tende al numero algebrico irrazionale chiamato sezione aurea o numero di Fidia.
In termini matematici:
dove
Naturalmente il rapporto tra un numero di Fibonacci e il suo successivo tende al reciproco della sezione aurea
.
.
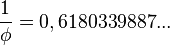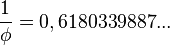Per valgono le seguenti relazioni:
valgono le seguenti relazioni:- a)
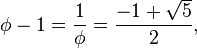
- b)
Si ha che l'-esimo numero di Fibonacci si può esprimere con la formula:
-esimo numero di Fibonacci si può esprimere con la formula:
La Golden Ratio continua ad aprire nuove porte nella nostra comprensione della vita e dell'universo. E' apparsa nella scoperta di Roger Penrose nel 1974 la "Penrose Tiles", (Tassellatura di Penrose), che è formata da due tasselli che possono ricoprire un piano solo aperiodicamente, ed è apparsa di nuovo nel 1984 nella disposizione molecolare tridimensionale degli atomi dei quasi-cristalli.
Mentre entriamo nel 21° secolo, il numero aureo Φ sembra avere una rinascita per integrare la conoscenza in una vasta gamma di campi di studio, tra cui il tempo e la fisica quantistica.
Questo prezioso "gioiello irrazionale" sembra sempre più indicare l’armonia nell’universo macro e micro.
Esiste uno stretto collegamento tra matematica frattale, numeri di Fibonacci e Φ e tutto sembra funzionare secondo questi parametri. La fisica quantistica ci dice che alla base della materia esiste un nucleo di energia sottile che vibra a frequenza specifica ed esso è detto stringa. La sua frequenza di vibrazione determina la modalità di aggregazione della materia a costituire una forma ed esiste quindi una relazione tra frattali, serie di Fibonacci e stringhe. Esistono connessioni tra la serie numerica di Fibonacci e i numeri delle dimensioni spazio temporali delle stringhe e questi numeri sono il doppio dei numeri di Fibonacci D = 2F.
Sempre più quindi le nuove scoperte sembrano essere in relazione con Φ, con questo "numero d'oro" o "numero magico", insomma con questo "gioiello irrazionale" che insieme alla successione di Fibonacci sembra davvero guidare l'armonia dell'universo.
Rappresentazione bidimensionale dello Spazio-Tempo
Nota¹ Altre proprietà matematiche della Successione di Fibonacci qui
Fonti:
From the book:
I numeri magici di Fibonacci di Keith Devlin
The Golden Ratio di Livio Mario
From website:
https://archive.org/details/divinaproportion00paci (manoscritto di Luca Pacioli)
http://www.goldennumber.net/
http://www.mathsisfun.com/numbers/golden-ratio.html
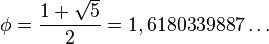
Nessun commento:
Posta un commento